L’esprit du Centre de Thérapie Atlantis


Sensibles aux concepts antiques de soins associant l’eau, l’architecture et les arts, nous nous sommes interrogés sur leur historique.
Les anciens, par l’observation, avaient cherché ce qui reliait le monde minéral, végétal, humain et l’univers dans lequel ils vivaient. Ils avaient défini une universalité de canons d’harmonie.
Les égyptiens, les grecques et les romains utilisaient des proportions communes.
Les mathématiques devenaient un langage universel qui s’étendait à tous ces mondes et à toutes ces civilisations.
Ce qui dépassait la réalisation de l’homme était considéré d’origine divine.
Le mathématicien Léonardo Fibonacci au XII ème siècle décrit la suite qui porte son nom.
Le moine Luca Pacioli, en 1509, a défini la divine proportion dans son ouvrage illustré par Léonard de Vinci.
A travers les siècles, de nombreux mathématiciens et savants se sont penchés sur cette proportion.
Ce n’est qu’au XIX ème siècle qu’est apparu le terme de nombre d’or qui regroupe toutes ces notions mathématiques appliquées depuis l’antiquité. Du nombre d’or découle la construction géométrique de la spirale d’or.
Nous avons décidé d’intégrer modestement ces éléments dans le projet d’un centre de thérapie et de recherche dédié à une forme de soins dans l’eau : l’Ostéopathie en milieu aquatique.
Nous allons vous relater quelques grands évènements qui ont jalonnés le chemin de l’antiquité à nos jours, de la divine proportion au nombre d’or et qui ont inspiré "l’esprit du Centre de Thérapie Atlantis ».
Ordonnancement de la nature
La géométrie sacrée

De tout temps, l’homme, intégré à la vie sur terre, a essayé de comprendre, d’analyser, de reproduire et de partager la beauté du monde minéral, végétal et animal qui l’entourait.
Les mathématiques, par leur universalité, ont permis de dépasser les langages, les cultures et les civilisations.
C’est ainsi que le concept de « géométrie sacrée » a été traduit dans le monde architectural et artistique.
Son expression est manifeste dans les lieux sacrés (temples, églises, mosquées, synagogues…) par certaines formes géométriques reproductibles avec des outils simples et agencées de manière répétitive jusqu’à former des structures complexes remarquables (rosace d’une église, façade du Parthénon à Athènes…).
Certains courants pensent que le monde a été créé selon un plan géométrique qui peut être retrouvé sur un plan, à la fois, microscopique et macrocospique.
Plutarque (philosophe romain 46 / 125 a.p. J-C) a attribué cette découverte à Platon (philosophe grec -428 / -348 av. J-C) et a écrit : "Platon a dit que Dieu crée de façon géométrique constamment et continuellement » (Convivialium disputationum, liber 8,2).
Le «prince des mathématiques » Carl Friedrich Gauss (1777 / 1855) s’est approprié les propos de Platon en disant "Dieu arithmetises ».
La géométrie sacrée s’appuie sur le nombre d’or : PHI ou Φ.
Ce nombre irrationnel est désigné par la lettre φ (phi) de l'alphabet grec en l'honneur de Phidias (v. - 490 - 430 av. J.-C.), sculpteur et architecte grec du Parthénon.
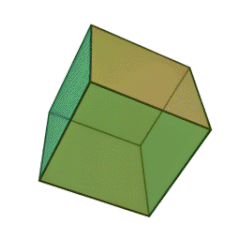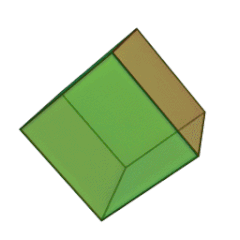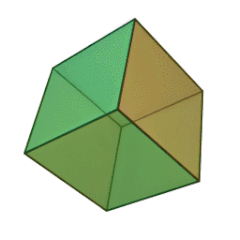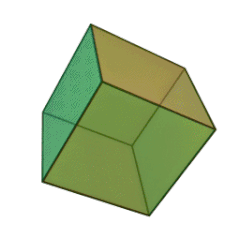
Le cube de Métatron est une figure géométrique qui est utilisée en géométrie sacrée et qui contient en lui les Cinq Solides de Platon.
Ce symbolisme a été utilisé dans de nombreuses cultures.
La proportion divine
Aux alentours de 1498, Luca Pacioli, moine italien, a écrit un livre de mathématiques « De divina proportione » (De la proportion divine) qui a été illustré par son ami Léonard de Vinci. Sa publication date de 1509.
Il traite de la la proportion mathématique (le titre renvoie au nombre d'or) et de son application en géométrie, dans les arts et en architecture. Son succès a dépassé le cercle des mathématiciens, notamment dans le domaine de l’art.

Le nombre d'or
Le nombre d'or (ou section dorée, ou proportion dorée, ou encore divine proportion) est une proportion, définie initialement en géométrie comme l'unique rapport a/b entre deux longueurs a et b telles que le rapport de la somme a + b des deux longueurs sur la plus grande (a) soit égal à celui de la plus grande (a) sur la plus petite (b) c'est-à-dire lorsque :
La première mention connue de la « division en extrême et moyenne raison » apparaît dans les Éléments d’Euclide (-325 -265 av JC et contemporain d’Archimède : -287 -212 av. J-C).
Ce nombre irrationnel désigné par la lettre φ (phi) est l'unique solution positive de l'équation x2 = x + 1. Il vaut :


L'histoire de cette proportion n'a pas pue être déterminée avec certitude.
Le nombre d’or fait partie des proportions de la grande pyramide de Khéops du plateau de Gizeh près du Caire en Egypte qui a inspirée la pyramide du Louvre de Paris.
Après Luca Pacioli, la vision de « De divina proportione » se développe et s'enrichit d'une dimension artistique, principalement au cours des XIX ème et XX ème siècles où naissent les termes de « section dorée » et de
« nombre d'or ».

La Suite de Fibonacci
Leonardo Fibonacci (v. 1175 v. 1250) est un mathématicien italien connu pour "la suite de Fibonacci". Mais il a, aussi, fait le lien entre le savoir mathématique des Arabes, notamment des chiffres indo-arabes, et l'Occident.
En mathématiques, "la suite de Fibonacci" est une suite d'entiers dans laquelle chaque terme est la somme des deux termes qui le précèdent. Elle commence par les termes 0 et 1 si on part de l'indice 0, ou par 1 et 1 si on part de l'indice 1.

Cette suite est liée au nombre d'or, φ, Φ, (phi) : 1,6180339…
En effet le rapport entre un terme et le terme précédent s’approche de la valeur φ d’autant plus que le terme est élevé.
F6/F5 = 8/5 = 1,6.
F7/F6 = 13/8 = 1,625
F11/F10 = 89/55 = 1,6181818
F16/F15 = 987/610 = 1,618032 …
Le Sanctuaire d'Asclépios (ou Esculape, dieu gréco-romain de la médecine) est un haut-lieu de la médecine grecque, situé en Argolide.
Durant l'Antiquité, les pèlerins accouraient de toute la Grèce pour se faire soigner dans le sanctuaire d'Asclépios, dieu guérisseur. Ce lieu abritait des médecins très réputés.

Le Théâtre d’Epidaure fait partie du site et intègre le nombre d’or dans sa construction.
Ce théâtre comporte :
-
13 escaliers
-
21 rangées de gradins au niveau supérieur
-
34 rangées de gradins au niveau inférieur
-
Soit 55 rangées de gradins
13, 21, 34 et 55 sont les termes F7 à F10 de la suite de Fibonacci reliée au nombre d'or.
La quine des bâtisseurs
Dans la construction, les bâtisseurs avaient, avant toute chose, le souci des proportions.
Leur référence était la « quine » ou canne ou pige et la corde à douze nœuds.
La quine était composée par les éléments suivants : paume, palme, empan, pied ou coudée.
Chaque élément est égal au précédent multiplié par φ.
Chaque élément est égal à la somme des deux précédents.
Ces proportions étaient étalonnées au nombre d’or.
Il s’agit donc d’une suite de Fibonacci que nous retrouvons dans la constitution d'un pentagone régulier.




La spirale d'or

Les carrés de Fibonacci en spirale s'ajustent ensemble pour former la spirale de Fibonacci. Ils sont créés en dessinant des arcs de cercle reliant les coins opposés de carrés constituant un pavage de Fibonacci.
Celui-ci utilise des carrés de tailles 1, 1, 2, 3, 5, 8, 13, 21, 34 …termes de la suite de Fibonacci.
La spirale de Fibonacci s’approche de la spirale d’or qui est créée en partant d’un rectangle d’or dans lequel la longueur est légale à la largeur + φ et en dessinant des arcs de cercle reliant les coins opposés de carrés, dont les côtés sont égaux à la longueur du rectangle.
Chaque nouvel apport d'un carré redonne un rectangle d'or.
A
Le Pentagone Régulier
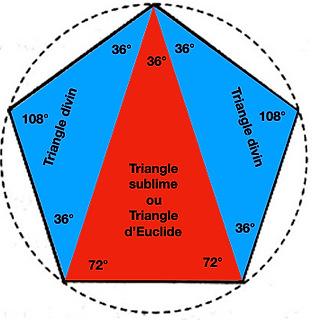
La construction d'un pentagone régulier à la règle et au compas est une des premières constructions (après le triangle équilatéral et le carré) non triviale réalisable grâce aux axiomes d’Euclide.
Les pythagoriciens (Pythagore : -580 -495 av. JC) connaissaient déjà une construction du pentagone à l'aide de triangles isocèles issus du nombre d'or:
-
le triangle d’or ou triangle sublime ou triangle d’Euclide tel que AB = AC et AB/BC = φ.
-
et le triangle divin ou gnomon d'or ou triangle d'argent ou, pour certains auteurs, triangle d'or obtus
tel que AD = DB = AE = EC et AD/AB = 1/φ
Euclide propose une construction d'un pentagone régulier inscrit dans un cercle donné.
Mais d'autres méthodes de construction plus rapides existent.
D'autres mathématiciens ou géomètres proposent aussi des constructions approchées réalisables avec un seul écartement de compas. C'est le cas par exemple d'Abu l-Wafa dans son Livre sur l’indispensable aux artisans en fait de construction (xe siècle), ou de Mathias Roriczer dans sa Geometria deutsch (1486), construction reprise par Albrecht Dürer (1525).

B
C
D
E
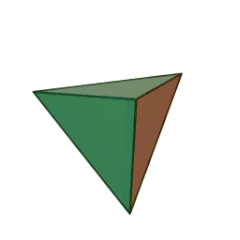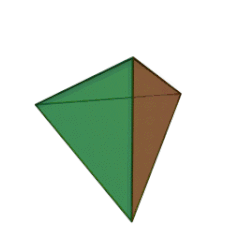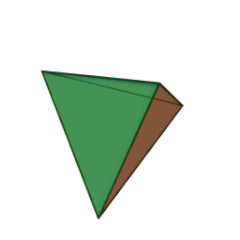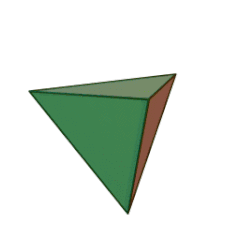
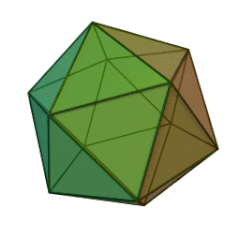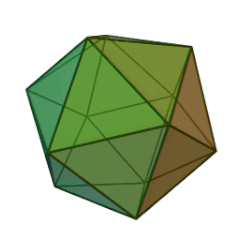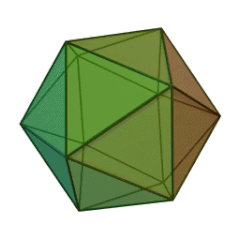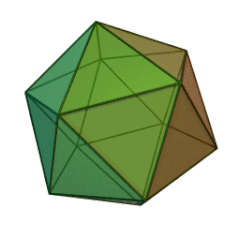
Les Solides de Platon
Depuis les mathématiques grecques, les solides de Platon furent un sujet d’étude des géomètres en raison de leur esthétique et de leurs symétries.
Leur nom, donné en l’honneur du philosophe grec Platon, rappelle une de ses théories, associant quatre d’entre eux aux quatre éléments de l’ancienne physique dans le dialogue Timée (env. 358 av. J.-C.).
Le nombre de faces du solide régulier, 4, 6, 8, 12, ou 20, est dans le préfixe du nom du solide :
Chaque solide de Platon répond à la formule d'Euler, démontrée en 1752 par le mathématicien suisse Leonhard Euler, obtenue avec un nombre F de faces, A d'arêtes et
S de sommets :
F + S – A = 2
L'homme de Vitruve de Leonard de Vinci

L’Homme de Vitruve (ou le proporzioni del corpo umano secondo Vitruvio en italien, les proportions du corps humain selon Vitruve) est un célèbre dessin annoté, réalisé vers 1490 à la plume, encre et lavis sur papier, par le peintre florentin Léonard de Vinci (1452-1519), d'après une étude de l’important traité d'architecture antique De architectura (au sujet de l’architecture) rédigé en -15 par l'architecte ingénieur romain Vitruve (v-90-v-15), et dédié à l’empereur romain Auguste.
Cette célèbre représentation des proportions idéales parfaites du corps humain s'inscrit dans un cercle (centre : le nombril) et un carré (centre : les organes génitaux) (symbolique du cercle et du carré).
L’Homme de Vitruve est un symbole allégorique emblématique de l’Humanisme, de la Renaissance, du rationalisme, de « L'Homme au centre de tout, l'Homme au centre de l’Univers », de la mesure et de la représentation du monde.
L'Homme de Vitruve a fait le lien symbolique entre de nombreuses sciences universelles étudiées par Léonard de Vinci : art, anatomie, géométrie, mathématiques, cosmologie, philosophie, métaphysique, mystère (christianisme), Dieu….
Vitruve cite « Pour qu’un bâtiment soit beau, il doit posséder une symétrie et des proportions parfaites comme celles qu’on trouve dans la nature ».
L'original appartient depuis 1822 aux Gallerie dell'Accademia de Venise.
Le nœud de l'infini tibétain
Le Nœud infini est un symbole bouddhiste tibétain représentant le mouvement de ce qui est éternel et des chemins spirituels qui s’entrelacent dans le temps. Il évoque la sagesse et la compassion. Le haut et le bas du symbole symbolisent l’interaction des forces opposées et duelles, qui finalement se rejoignent et s’unissent dans l’univers. Il représente également l’inséparabilité du Vide et de la réalité de l’existence.


L'œil d'Horus ou Oudjat
Symbole de la lumière, de la connaissance et de la santé, c’est l’œil du faucon qui voit tout et qui voit au-delà du visible.
Les jardins de la Villa Borghese
Les jardins de la Villa Borghèse furent réalisés par Flaminio Ponzio sur les plans du cardinal Scipione Borghese pour agrémenter la villa suburbaine qu'il s'était fait construire afin d'y abriter sa collection d'art. En 1605, il fait transformer un vignoble en luxueux jardins verdoyants et ombragés alimentés de nombreuses fontaines. Ce parc est le plus important construit à Rome depuis l'époque antique. L'ensemble de la villa fut terminé en 1633.
Le premier jardin à l'anglaise de Rome, près de la villa Borghèse est dû au peintre et architecte écossais Jacob More. Les jardins actuels datent du xixe siècle et ont été réalisés dans le style anglais.
Henri Voogd les immortalisera dans un tableau qui a inspiré la décoration murale qui vous accueille dans notre salle d'attente.

Jacob More
Jacob More (né à Édimbourg en 1740 et mort à Rome le 1er octobre 1793) est un peintre aquarelliste et dessinateur anglais, connu pour sa peinture de paysages panoramiques. Il est également connu comme More de Rome.
Il est aussi scénographe et architecte de jardins. Le premier jardin à l'anglaise de la ville, près de la villa Borghèse lui est dû.
En peinture, il se spécialise dans les paysages classiques et lumineux dans le style du peintre français Claude Gellée ou Gelée, dit « le Lorrain » (né vers 1600 et mort à Rome le 23 novembre 1682), célèbre pour ses paysages historiques. Il est également influencé par Gaspard Dughet et Claude Joseph Vernet.
Hendrik Voogd
Hendrik Voogd, né le 10 juillet 1768 à Amsterdam et mort le 4 septembre 1839 à Rome, est un peintre et graveur néerlandais principalement actif en Italie.
En 1807, il a peint les jardins de la Villa Borghese à Rome en fin d’après-midi : le soleil projette de longues ombres et les arbres s’illuminent contre le ciel.
Ce tableau de 101,5cm de hauteur sur 138,5cm de largeur est exposé au Rijksmuseum d’Amsterdam qui mentionne dans son catalogue :
Paysage italien avec pins parasols ou pins dans le jardin de la Villa Borghèse à Rome. En arrière plan la villa Giulia et le monte Mario.
Voogd a été baptisé « Hollandse Claude » par ses contemporains en hommage au peintre français dit « le Lorrain » qui inspira aussi Jacob More.